Билет №14

Площадь многоугольной фигуры. Формулы площади треугольника.

Герон

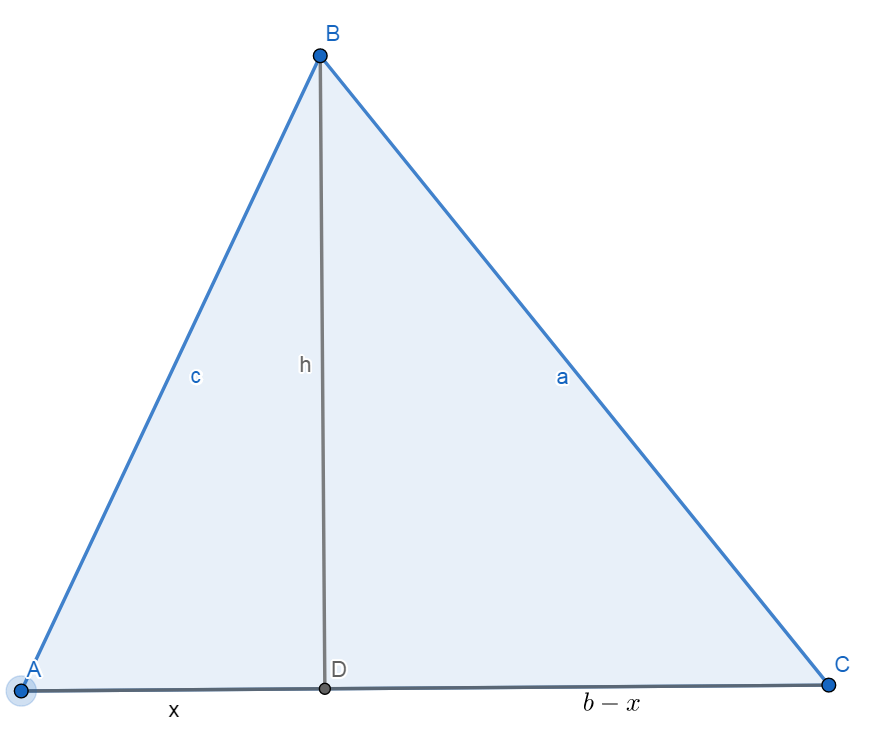
Запишем теорему Пифагора:

\[h^2 = c^2 - x^2 = a^2 - (b - x)^2; \\ (b - 2x)b = a^2 - c^2; \\ b - 2x = \frac{a^2 - c^2}{b}; \\ x = \frac{b^2 - a^2 + c^2}{2b}\]

Распишем то выражение:

\[h^2 = c^2 - x^2 = c^2 - (\frac{b^2 - a^2 + c^2}{2b})^2 = \\ = \frac{2bc - b^2 + a^2 - c^2}{2b} \cdot \frac{2bc + b^2 - a^2 + c^2}{2b} = \\ = \frac{a^2 - (b - c)^2}{2b} \cdot \frac{(b + c)^2 - a^2}{2b} = \\ = \frac{(a + c - b)(a + b - c)(a + b + c)(b + c - a)}{(2b)^2} = \\ = \frac{2^4 \cdot p(p - a)(p - b)(p - c)}{4b^2} = \frac{4 \cdot p(p - a)(p - b)(p - c)}{b^2} \Rightarrow \\ \Rightarrow h = 2 \cdot \frac{\sqrt{p(p - a)(p - b)(p - c)}}{b} \Rightarrow \\ \Rightarrow S = \frac{b \cdot h}{2} = \sqrt{p(p - a)(p - b)(p - c)}\]