Билет №1

Замечательные точки треугольника.

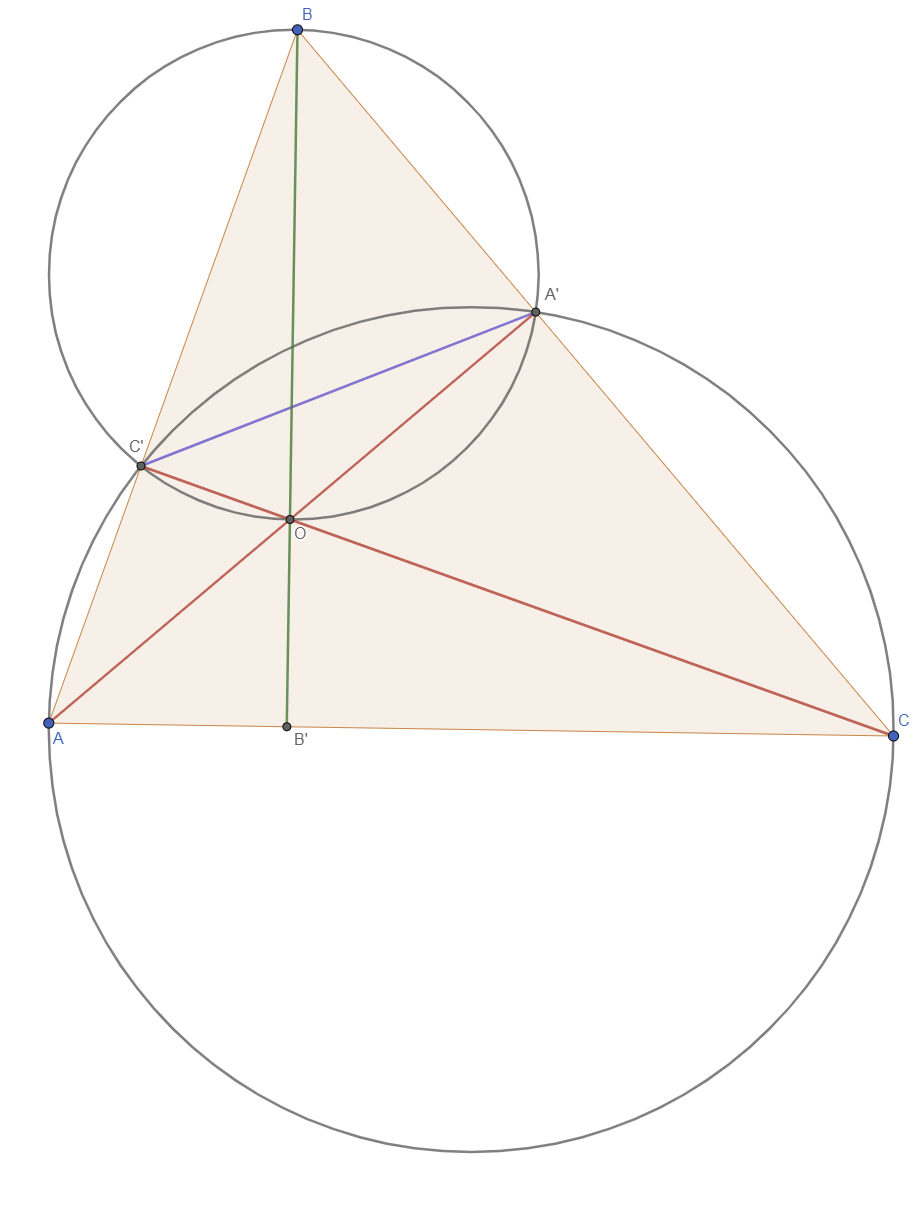
Точка пересечения высот

\(AA' и CC' - высоты\) \(O = AA' \cap CC'\) \(B' = BO \cap AC\)

Так как \(\angle AC'C = \angle AA'C = 90^{\circ}\), то \(A, A', C' и C\) лежат на одной окружности, тогда \(\angle ACC' = \angle AA'C'\)

Аналогично получаем, что \(A', O, C', B\) тоже лежат на одной окружности, значит \(\angle OBC' = \angle OA'C' \Rightarrow \angle ACC' = \angle OBC'\)

Также из вертикальности углов следует \(\angle BOC' = \angle COB' \Rightarrow \angle OB'C = \angle OC'B = 90^{\circ}\)

Аналогичный разбор случая тупого треугольника

Центр тяжести

Приведённое ниже доказательство взято с сайта e-maxx.ru, материалы, которого выложены под лицензией Public Domain.

Приведём здесь элементарное доказательство, не использующее теорию интегралов. Доказательство сводится к тому, чтобы показать, что центр масс треугольника лежит на одной из медиан; повторяя этот процесс ещё дважды, мы тем самым покажем, что центр масс лежит в точке пересечения медиан, которая и есть центроид. Разобьём данный треугольник \(T\) на четыре, соединив середины сторон, как показано на рисунке:

Четыре получившихся треугольника подобны треугольнику \(T\) с коэффициентом \(\frac{1}{2}\). Треугольники №1 и №2 вместе образуют параллелограмм, центр масс которого \(c_{12}\) лежит в точке пересечения его диагоналей (поскольку это фигура, симметричная относительно обеих диагоналей, а, значит, её центр масс обязан лежать на каждой из двух диагоналей). Точка \(c_{12}\) находится посередине общей стороны треугольников №1 и №2, а также лежит на медиане треугольника \(T\):

Пусть теперь вектор \(\vec{r}\) - вектор, проведённый из вершины \(A\) к центру масс \(c_1\) треугольника №1, и пусть вектор \(\vec{m}\) — вектор, проведённый из \(A\) к точке \(c_{12}\) (которая, напомним, является серединой стороны, на которой она лежит):

Наша цель — показать, что вектора \(\vec{r}\) и \(\vec{m}\) коллинеарны. Обозначим через \(c_3\) и \(c_4\) точки, являющиеся центрами масс треугольников №3 и №4. Тогда, очевидно, центром масс совокупности этих двух треугольников будет точка \(c_{34}\), являющаяся серединой отрезка \(c_3 c_4\). Более того, вектор от точки \(c_{12}\) к точке \(c_{34}\) совпадает с вектором \(\vec{r}\). Искомый центр масс \(c\) треугольника \(T\) лежит посередине отрезка, соединяющего точки \(c_{12}\) и \(c_{34}\) (поскольку мы разбили треугольник \(T\) на две части равных площадей: №1-№2 и №3-№4):

Таким образом, вектор от вершины \(A\) к центроиду \(c\) равен \(\vec{m} + \vec{r}/2\). С другой стороны, т.к. треугольник №1 подобен треугольнику \(T\) с коэффициентом \(1/2\), то этот же вектор равен \(2 \vec{r}\). Отсюда получаем уравнение:

\(\vec{m} + \vec{r}/2 = 2 \vec{r},\) откуда находим:

\(\vec{r} = \frac{2}{3} \vec{m}.\) \(\vec{r}\) и \(\vec{m}\) коллинеарны, что и означает, что искомый центроид \(c\) лежит на медиане, исходящей из вершины \(A\). Более того, попутно мы доказали, что центроид делит каждую медиану в отношении \(2:1\), считая от вершины.